Oct 2023: Rev 1.1
The Hill Sphere
There are two rival definitions of “gravitational sphere of influence”
- the Laplace sphere: suitable for objects at rest relative to central body
- the Hill sphere: suitable for objects orbiting central body
Consider a small thing orbiting a big thing Let’s call the small thing “Earth” and the big thing “Sun” Consider an even smaller thing, called “spacecraft”, moving in their joint gravity – when is it a better approximation to say the spacecraft is orbiting the Earth vs orbiting the Sun?
Answer: when you are within E's Hill Sphere with respect to S:
r < R (m_E / 3m_S )(1/3),
then it makes more sense to say you’re in orbit around Earth.
`Orbit' may be elliptical (bound) or hyperbolic (unbound). When you're doing a fast flyby
of some planet - say Mars - just above its atmosphere, deep in its gravity well,
it doesn't make much mathematical sense to say you're in solar orbit just
because you have escape velocity relative to the planet. (Yes, I know, people, including
expert astrodynamicists, often do say this. I just think they are wrong.) In the way I construe
the situation, you are in a hyperbolic orbit around the planet until you pass
the Hill Sphere boundary, at which point you enter solar orbit. (More strictly:
it makes more sense, and is more mathematically convenient,
to think of you as being in the hyperbolic Mars-centered orbit
within the Hill Sphere and an elliptical Sun-centered orbit beyond it. Obviously
`reality' is that the concept of being in orbit about one thing or other
is only an approximation as you are always moving in the combined field of all
gravitating bodies.)
The Earth-Moon System
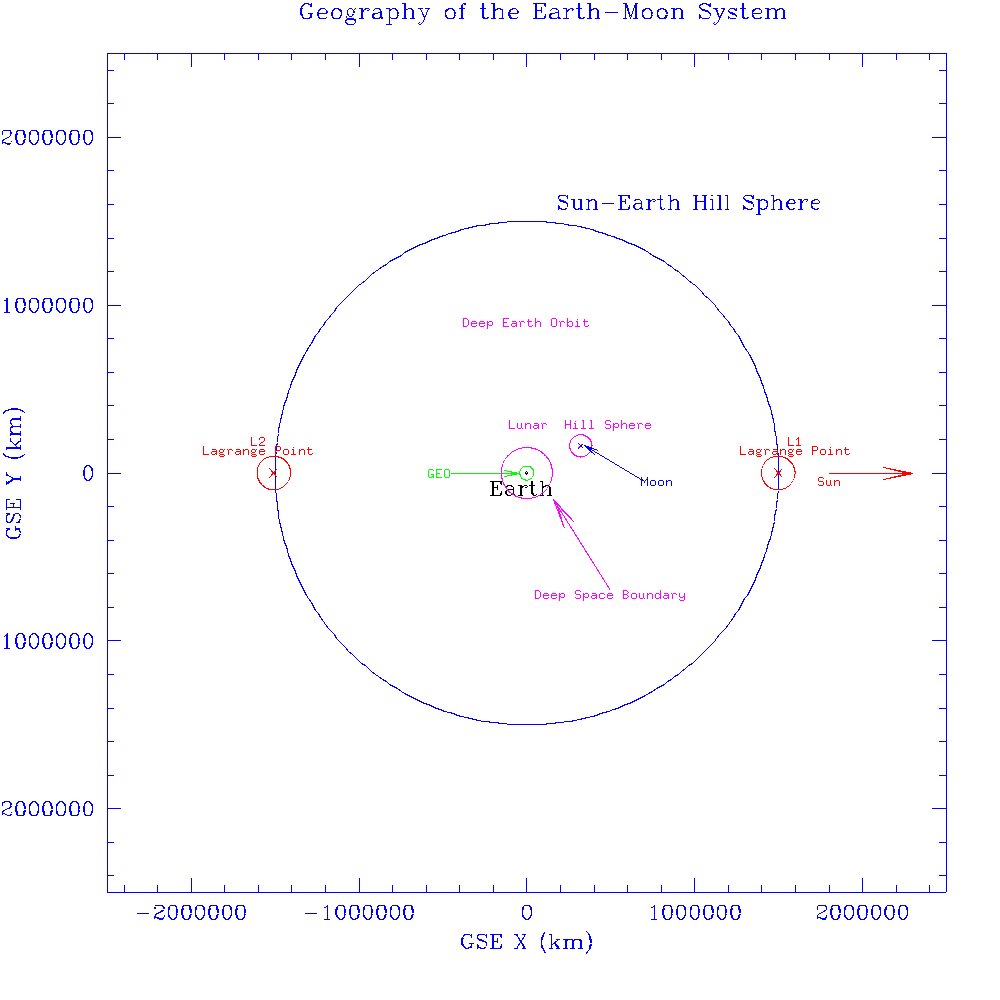
Here is a map of the Earth-Moon system (the location of the Moon is shown as it was on Dec 21, 1968). The map is in geocentric solar ecliptic coordinates in which the Earth-Sun line is fixed and is the X-axis. The SEL1 and SEL2 Sun-Earth Lagrange points are along this axis. Here you can see the small size of the lunar Hill sphere (with respect to the Earth) compared to the Earth's Hill sphere with respect to the Sun. You can also see the relatively tiny size of the green circle denoting GEO: the vast majority of artificial Earth satellites are within this circle. Also illustrated (magenta circle centered on Earth) is the EL1:4 deep space boundary used in this catalog. There's a lot of 'Earth orbit' beyond this boundary!